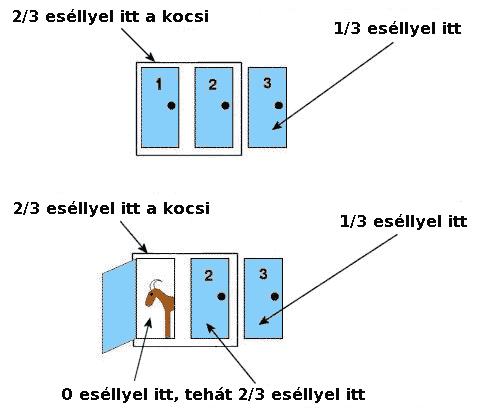
#290 A Monty Hall-paradoxon az egyik legérdekesebb matekos feladvány. Amerikában 1963 óta fut egy televíziós vetélkedő Let’s make a deal! néven, amit a paradoxon névadója, Monty Hall vezetett egy időben. A műsor végjátékában a játékosok választani kényszerülnek 3 csukott ajtó közül: 2 ajtó mögött kecske van, a 3. viszont egy autót rejt. A játékos választását követően Monty kinyitja az egyik kiválasztásra nem került ajtót, amelyik mögött egy kecske van, majd megkérdezi a játékost a két zárt ajtóra mutatva hogy akarja-e esetleg módosítani a választását. A racionalitás azt sugallná, hogy felesleges változtatni, viszont a valószínűségszámítás és a statisztika rácáfol erre: akik nem változtatták meg a műsorban a döntésüket azok kb. 1/3-a nyert, akik viszont a másik ajtóra voksoltak azok 2/3-a. A Wikipedia ábrája picit segít a megértésben: ha kitartunk eredeti döntésünk mellett, akkor azt feltételezzük, hogy az elsőnek kiválasztott ajtó mögött autó lesz. Az ajtók 2/3-a mögött kecske van, tehát a nyerési esély 1/3. Miután kinyitotta a műsorvezető az egyik ajtót és megmutatta a kecskét a valószínűségek nem változtak, tehát 1/3 az esélye annak, hogy az elsőre választott ajtó mögött van az autó, viszont ekkor a két másik ajtó közül már csak az egyik van csukva, annak a valószínűsége pedig, hogy az autó valamelyik csukott ajtó mögött van 100%, ezért 2/3 valószínűséggel a másik csukott ajtó mögött van a kocsi.





